If you've already tackled question 8 (proving that \(\sum_{k=1}^n\frac1k\) diverges), then this should be a piece of cake! Again the trick is to visualise each term \(\frac1{k^2} \) as the area of a recangle of dimensions \(1 \times \frac1{k^2}\):

As you can see, \(\sum_{k=1}^\infty\frac1{k^2} \) simply corresponds to the sum of all the rectangles' area. Now if you consider the function \(x \rightarrow \frac1 {x^2}\), you'll notice that the area under the curve starting at \(x=1\) is strictly greater than the orange area (first rectangle excluded):

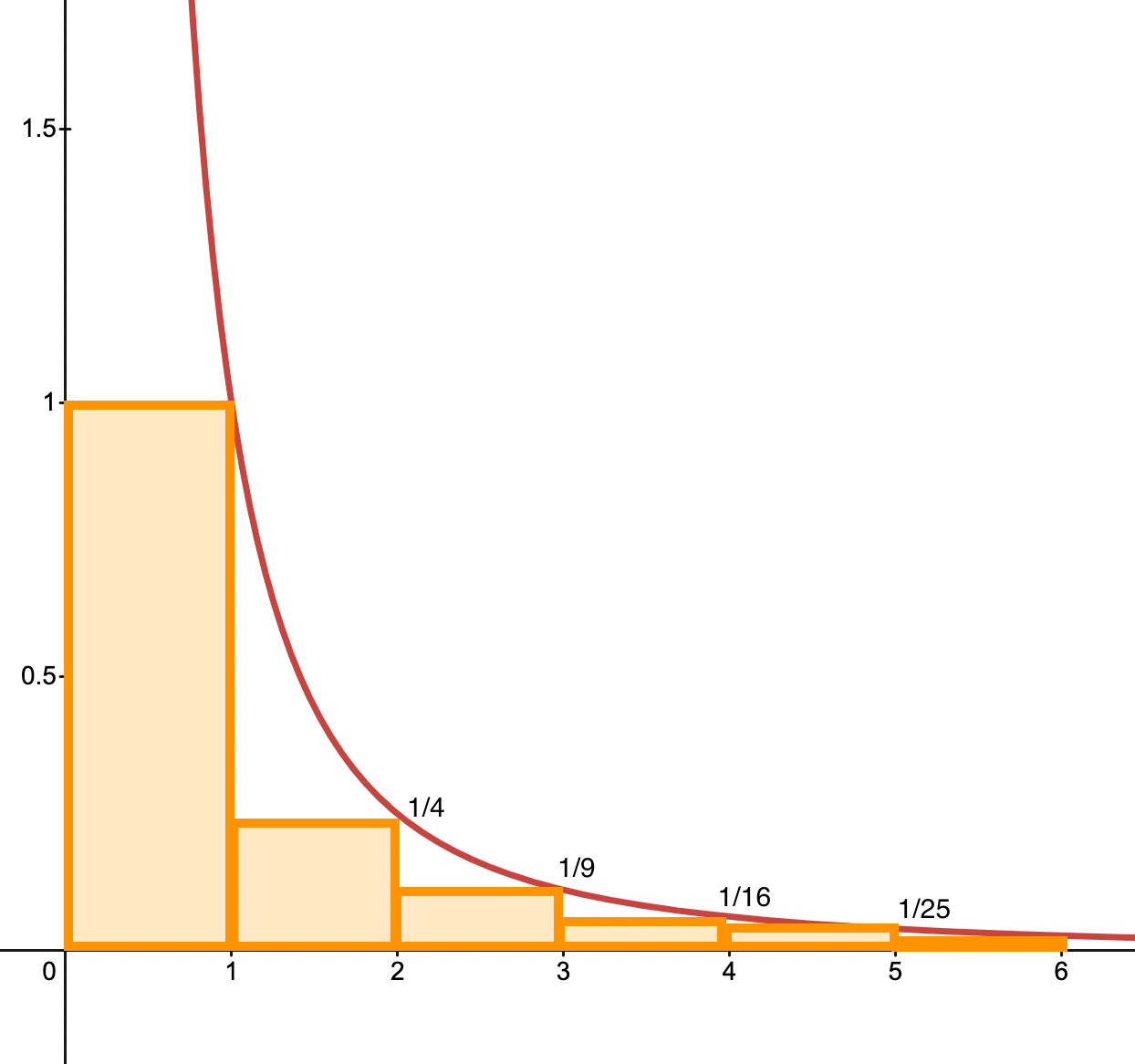
Hence, if you're able to show that the area under the curve \(x \rightarrow \frac1 {x^2}\) on \((1, \infty)\) is bounded, you win.

The area under the curve \(x \rightarrow \frac1 {x^2} \) from \(x=1\) to \(x=N\) is simply: $$ \int_1^N {\frac1 {x^2}} \, dx = \bigg[-\frac1x\bigg]_1^N $$ $$ = 1 - \frac1N$$ which tends to \(1\) as \(N \rightarrow \infty\). Hence \(\sum_{k=1}^\infty\frac1 {k^2} \) is bounded by \(1 + \) {area of the first rectangle} \(= 2\).