Sketch the graph of x^4 + y^4 = 1

Question 7

Sketch the graph of $x^4 + y^4 = 1$.

When sketching a function's graph, you typically want to focus on the following characteristics:

Any axis of symmetry.

Where the graph crosses the $x$ and $y$ axes.

Where the extrema are and their nature (maxima, minima or inflection points).

The slope of the graph between the extrema.

The asymptotic values of the function.

Before diving into each of these though, first note that $x^4+y^4=1$ is only defined on $[-1,1]$. We can thus safely ignore the last point.

1) Axes of symetry

It's easy to see that if $(x,y)$ is a solution, then:

$(- x,y)$ is a solution, so the graph is symmetrical along the $y \text{-axis}$.

$(x,-y)$ is a solution, so the graph is symmetrical along the $x \text{-axis}$.

$(y,x)$ is a solution, so the graph is symmetrical along the line $y=x$.

2) Where the graph crosses the $x$ and $y$ axes

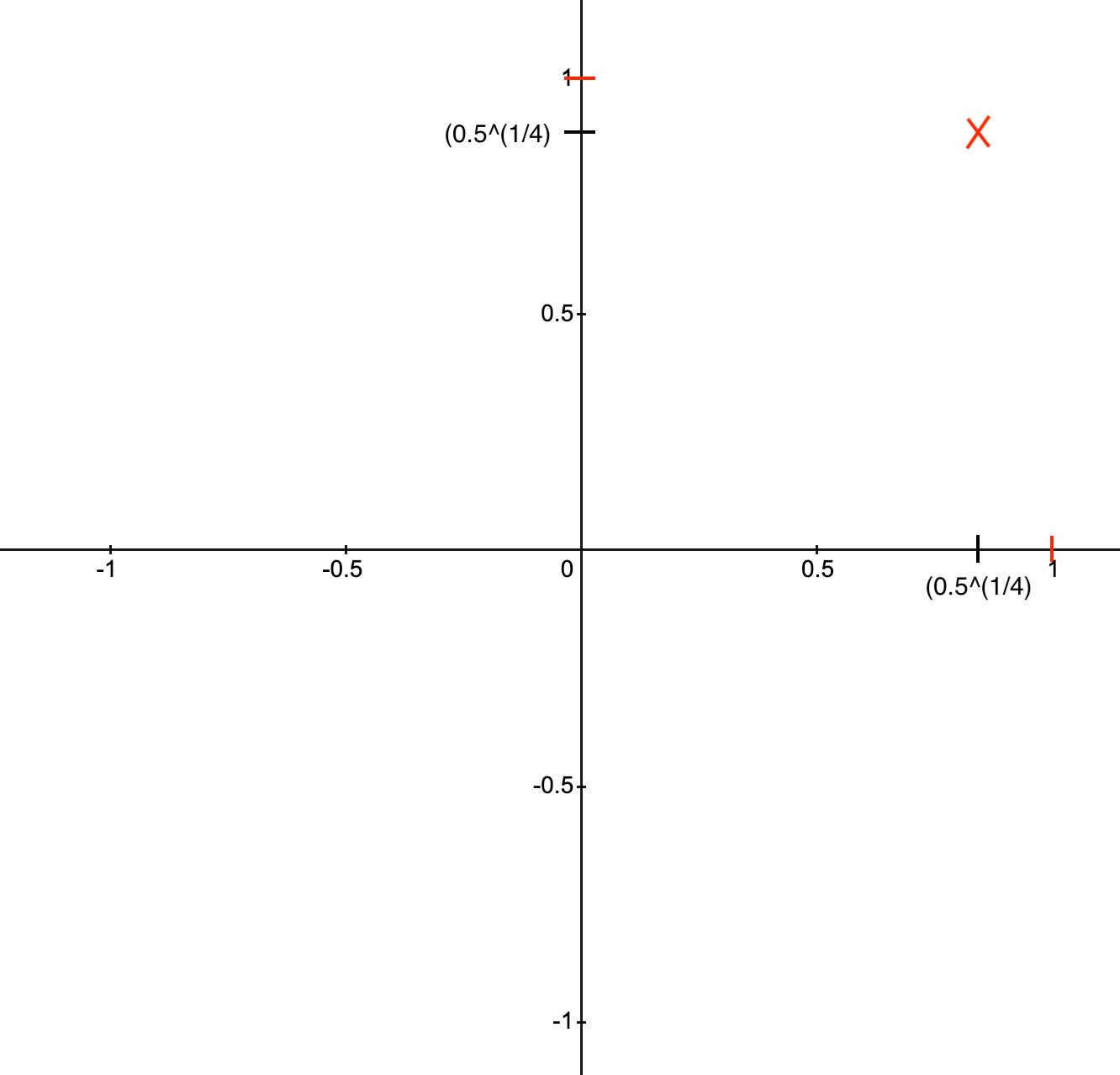
When $x=0$, $y=\pm 1$ and when $y=0$, $x=\pm 1$, so you can already start by sketching these $4$ points. Given that the graph is also symmetric along the line $y=x$, it is worth finding out where it intersects this line. Setting $y=x$, we get: $$ 2x^4=1 \iff x^4 = \frac12$$ $$ \iff x = \pm \bigg(\frac1 { 2 }\bigg)^\frac14 $$ Quick trial and error tells you $|x|$ is between $0.8$ and $0.9$: $$ 0.8^4 = 0.64^2 \leq 0.7^2 = 0.49 $$ $$ 0.9^4 = 0.81^2 \geq 0.8^2 = 0.64 $$

3) The extrema

To find the extrema, simply differentiate the equation with respect to $x$ and isolate $dy/dx$. $$ \frac { d( x^4+y^4 ) } { dx } = \frac { d(1) } { dx }$$ $$ 4x^3 + 4y^3 \times y' = 0$$ $$ y' = -\frac { x^3 } { y^3 } \text{ for } y \neq 0 $$ And we see that $y'=0$ for $x=0$. So the inflection points are at $ (0,\pm1) $. Given that $x$ and $y$ are bounded by $1$, we also know $ (0, 1)$ must be a maximum.

4) The slope of the graph between the extrema

There are four things to note here:

$y \rightarrow 0$, $y' \rightarrow \infty$.

$y' \leq 0$ in the first quadrant.

$y'=-1$ for $x=y$.

$y'$ becomes increasingly negative as $x$ increases from $0$ to $1$.

This should be enough information to let you finish sketching the graph.